カルマンフィルタによる構造振動系の同定．（1自由度系振動モデルを想定）
　なお，本プログラムは，MaTX公式サイトのMaTXユーザーズマニュアルの例題プログラムを参考にしています．

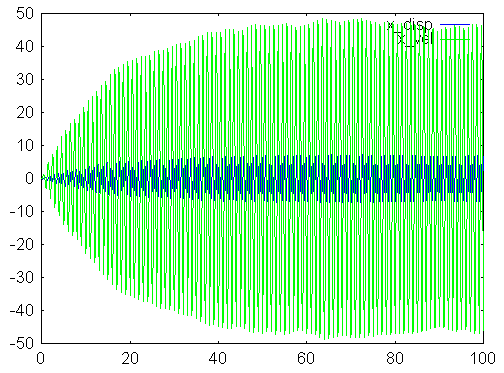
　カルマンフィルタが逐次推定した構造物の状態は，gnuplotにより以下のように出力されます．（青：変位，緑：速度）
　本プログラムでは観測値ypに2種類の正弦波（1.0Hz：振幅1，2.5Hz：振幅0.1）とランダム波（振幅をランダムに設定，最大振幅1.0）とを足し合わせて作った模擬観測波を用いていますが，概ね50秒程でカルマンフィルタの状態推定値が収束してくることがわかるでしょうか？

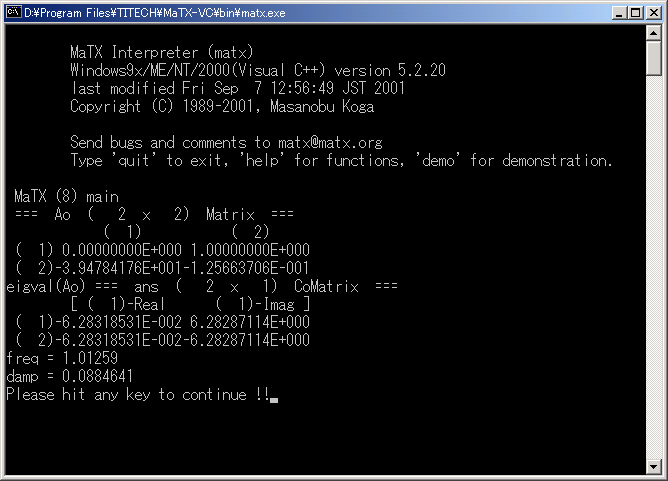
　以下はコンソール出力である．最終的に同定された構造物の振動特性値が出力されます．
　Aoは観測器（カルマンフィルタ）の状態マトリクス，eigval(Ao)はAoの固有値であります．以下，固有振動数（Hz），減衰比が出力されます．

　観測値（構造物の振動測定波形値）ypにA/D変換ボードからの測定値を用い，rtMaTX用にプログラムを書き換えれば，リアルタイム（オンライン）での同定が可能であるとのことです．

// karman.mm

Matrix Ao, Bo, Co, Ro, Qo, Ho;     // 観測器のパラメータ

Func void init_params()
{
  Matrix MM, CC, KK;
  Real f_s, d_s, m_s;

  f_s=2*PI;       // 初期値
  d_s=0.01;
  m_s=1.0;
  
  MM = [m_s];
  CC = [2*m_s*d_s*f_s];
  KK = [m_s*f_s^2];

  // 観測器のパラメータ
  Ao = [[0, 1]
        [-MM~*KK, -MM~*CC]];
  Bo = [[1]
        [MM~]];
  Co = [1, 1];
  Ro = [1];
  Qo = Co'*Co;
}

Func Matrix DRiccati(A, B, Q, R)
  Matrix A, B, Q, R;
{
  Matrix P, PP;
  Real eps;

  P = PP = I(A);          // 解 P の初期値
  eps = 1.0E-7;

  // 解が収束するまで繰り返す
  while (frobnorm(P - PP) > eps) {
    PP = P;
    P = Q + A'*P*A - A'*P*B*(R + B'*P*B)~ * B'*P*A;
    P = (P' + P)/2.0;   // P の対称性を回復
  }

  return P;               // 解 P を返す
}

Func void main()
{
  Matrix x0, AA;
  Array TC, XC, UC;
  Real freq, damp;

  void diff_eqs(), link_eqs(), init_params();

  init_params();

  print Ao;
  print "eigval(Ao)";
  print eigval(Ao);

  x0 = [0 0]';
  {TC, XC, UC} =
     Ode(0.0, 100.0, x0, diff_eqs, link_eqs, 0.1);
  AA = Ao-Ho*Co;
  freq = sqrt(-AA(2,1))/(2*PI);
  damp = -AA(2,2)/(2*sqrt(-AA(2,1)));
  print freq;
  print damp;
  mgplot(1, TC, XC, {"x_disp", "x_vel"});
  pause;
}

Func void diff_eqs(DX, t, X, UY)
  Real t;
  Matrix X, DX, UY;
{
  Matrix dxo, xo, yp, Po;

  xo = X(1:2,1);          // 観測器の状態
  yp = UY(1:1,1);         // 観測器への入力

  Po = DRiccati(Ao, Co, Qo, Ro); // DRiccati()を呼ぶ
  Ho = Po*Co'*Ro~;
  dxo = Ao*xo - Ho*yp;    // 観測器の状態方程式
  DX = dxo;
}

Func void link_eqs(UY, t, X)
  Real t;
  Matrix UY, X;
{
  Matrix yp, xo;

  xo = X(1:2,1);          // 観測器の状態

  yp = [sin(2*PI*1.0*t)+0.1*sin(2*PI*2.5*t)+(rand()-0.5)*2];        // 観測値
  UY = yp';
}